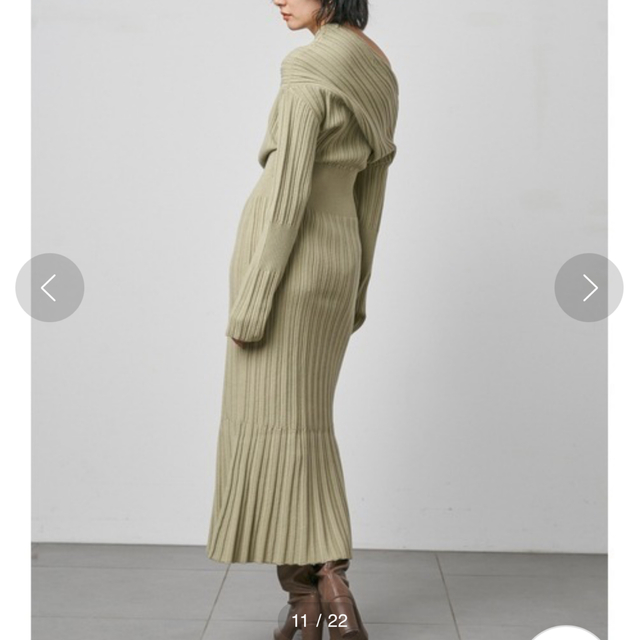
スナイデル ワンショルリブワンピース ミントなし伸縮性
ランキング37位ロングワンピース/マキシワンピース
通常価格(税込)
4,845円
送料無料(全国一律)
※条件により送料が異なる場合があります。
-
ご注意表示よりも実際の付与数・付与率が少ない場合があります(付与上限、未確定の付与等)
-
「PayPaySTEP」は、付与率の基準となる他のお取引についてキャンセル等をされたことで、付与条件が未達成となる場合があります。この場合、表示された付与数・付与率では付与されません。なお、詳細はPayPayステップのヘルプページでご確認ください。
ヤフー株式会社またはPayPay株式会社が、不正行為のおそれがあると判断した場合(複数の JAPAN IDによるお一人様によるご注文と判断した場合を含みますがこれに限られません)には、表示された付与数・付与率では付与されない場合があります。
各特典に設定された「付与上限」を考慮した数字を表示できないケースがございます。その場合、実際の付与数・付与率は表示よりも低くなります。各特典の付与上限は、各特典の詳細ページをご確認ください。
付与数は算定過程で切り捨て計算されている場合があります。付与数と付与率に齟齬がある場合、付与数の方が正確な数字になります。
-
-
原則税抜価格が対象です。特典詳細は内訳でご確認ください。
04/24〜05/14の間に発送予定
お届け日指定はできません
絞り込む
-
4.8
2023-10-22 09:49:00
tab*****さん
スナイデル ワンショルリブワンピース ミントなし伸縮性
予定した通り届きました。ありがたいことです。
-
4.7
2023-08-25 17:16:00
gar*****さん
スナイデル ワンショルリブワンピース ミントなし伸縮性
注文から届くまでスピーディ 梱包、配達も申し分ありませんでした。
-
4.6
2023-08-13 20:29:00
xpv*****さん
スナイデル ワンショルリブワンピース ミントなし伸縮性
無事届きましたありがとうございました、追跡出来るとありがたいと、思いました。
-
4.7
2023-07-29 21:27:00
rav*****さん
スナイデル ワンショルリブワンピース ミントなし伸縮性
迅速な対応して頂き有難う御座います。気持ち良くお取引させて頂きました。
-
4.6
2023-07-28 21:04:00
naj*****さん
スナイデル ワンショルリブワンピース ミントなし伸縮性
綺麗な梱包、説明書、案内文、とかなり信頼感を感じる配送をしていただきました。 有り難うございました。
-
4.5
2023-07-26 02:32:00
tvz*****さん
スナイデル ワンショルリブワンピース ミントなし伸縮性
いつもありがとうございます。又、宜しくお願い致します!
-
4.9
2023-04-04 20:50:00
yur*****さん
スナイデル ワンショルリブワンピース ミントなし伸縮性
配送も問題ないです。梱包も特に問題なかったです。素早い配送ありがとうございました
-
4.6
2023-03-27 16:08:00
lor*****さん
スナイデル ワンショルリブワンピース ミントなし伸縮性
梱包は、軽量物の為必要最小限の梱包で良かった。配送は、注文から中2日で受け取りで、大変良かった。対応は、最安値で購入出来、速く届き良かった。
該当するレビューコメントはありません
情報を取得できませんでした
時間を置いてからやり直してください。
商品説明
-
商品カテゴリ
-
JANコード/ISBNコード
C569477770
-
商品コード
077774965C
ワンショルリブワンピース
col...MNT
店頭にて購入。
一度のみ短時間使用しました。
状態は綺麗な方かと思います。
以下サイトより引用。
【モードだけど女性らしいディフォーメーションニット】
【Design/Styling】
ニットにカーディガンを巻いているような、フェイクレイヤードデザインのプルオーバー。左サイドには大胆な肩あきディテールを施し、ニットのボリュームとバランスを取りつつ、身体が華奢に見えるよう工夫しました。肩にかかるカーディガンがしなやかな色香を纏い、カジュアルなシルエットでも女性らしさが漂います。違う編み地のニットを組み合わせることで奥行きが生まれ、異素材ミックスの遊び心も表現しました。
【Fabric】
秋冬らしいふっくらとした柔らかなニットを使用しました。ワントーンのアイボリーと配色のブラウンの2色をご用意。
透け感:なし
裏地:なし
伸縮性:あり
光沢感:なし
生地の厚さ:やや厚手

SNIDEL(スナイデル)の「ワンショルリブワンピース(ワンピース ...

SNIDEL(スナイデル)の「ワンショルリブワンピース(ワンピース ...

SNIDEL - SNIDEL ワンショルリブワンピース ミントグリーンの通販|ラクマ
ストア情報
一品からでも全国送料無料でお届けします!
KEYWORDS
営業日カレンダー
定休日
| 日 | 月 | 火 | 水 | 木 | 金 | 土 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
| 日 | 月 | 火 | 水 | 木 | 金 | 土 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 |